Example of a coordinate transformation from z levels to density levels¶
Rebinning ty_trans to ty_trans_rho density levels¶
This transformation is commonly used for the purpose of decomposing the residual meridional overturning streamfunction into mean and eddy components. The mean is taken to be the time-mean Eulerian transport (time-mean in z coordinates), whilst the residual transport is the time-mean in density coordinates (density surface move in time). The eddy transport is the difference between the residual overturning streamfunction, and the Eulerian transport transformed from depth to density coordinates via the time-mean density.
Binning is the discrete version of this transformation from depth to density coordinates. We define target density bins, and for each bin we add the quantity to be binned from all cells with a density that satisfies that bin. In its simplest form, binning is creating a histogram.
We use three different binning methods: 1. xhistogram, which performs binning in exactly the way MOM5 does and is thus most appropriate for calculating eddy quantities (define edge of bins) 2. xgcm conservative binning (define edge of bins, but vertically interpolates so looks smoother than xhistogram) 3. Using density coordinate binning method of Lee et al. (2007) (define isopycnals to bin onto i.e. centre)
Compute times were calculated using the XXLarge (28 cpus, 128 Gb mem) Jupyter Lab on NCI’s ARE, using conda environment analysis3-22.10
[1]:
%matplotlib inline
import cosima_cookbook as cc
from cosima_cookbook import distributed as ccd
import matplotlib.pyplot as plt
import numpy as np
import xarray as xr
import glob
import cmocean.cm as cmocean
import xgcm
import logging
logging.captureWarnings(True)
logging.getLogger('py.warnings').setLevel(logging.ERROR)
from xhistogram.xarray import histogram
from dask.distributed import Client
[2]:
client = Client()
client
[2]:
Client
Client-1c9b3d66-9cab-11ed-8ab8-0000075dfe80
| Connection method: Cluster object | Cluster type: distributed.LocalCluster |
| Dashboard: /proxy/8787/status |
Cluster Info
LocalCluster
66f6e48f
| Dashboard: /proxy/8787/status | Workers: 4 |
| Total threads: 12 | Total memory: 48.00 GiB |
| Status: running | Using processes: True |
Scheduler Info
Scheduler
Scheduler-84082265-391c-4a64-a163-ba4d85ecd464
| Comm: tcp://127.0.0.1:42533 | Workers: 4 |
| Dashboard: /proxy/8787/status | Total threads: 12 |
| Started: Just now | Total memory: 48.00 GiB |
Workers
Worker: 0
| Comm: tcp://127.0.0.1:41425 | Total threads: 3 |
| Dashboard: /proxy/45695/status | Memory: 12.00 GiB |
| Nanny: tcp://127.0.0.1:45595 | |
| Local directory: /jobfs/70847928.gadi-pbs/dask-worker-space/worker-efqj0ut_ | |
Worker: 1
| Comm: tcp://127.0.0.1:42233 | Total threads: 3 |
| Dashboard: /proxy/46865/status | Memory: 12.00 GiB |
| Nanny: tcp://127.0.0.1:33981 | |
| Local directory: /jobfs/70847928.gadi-pbs/dask-worker-space/worker-xn_0uinn | |
Worker: 2
| Comm: tcp://127.0.0.1:44059 | Total threads: 3 |
| Dashboard: /proxy/37341/status | Memory: 12.00 GiB |
| Nanny: tcp://127.0.0.1:36705 | |
| Local directory: /jobfs/70847928.gadi-pbs/dask-worker-space/worker-__jr2vw7 | |
Worker: 3
| Comm: tcp://127.0.0.1:43221 | Total threads: 3 |
| Dashboard: /proxy/37185/status | Memory: 12.00 GiB |
| Nanny: tcp://127.0.0.1:33369 | |
| Local directory: /jobfs/70847928.gadi-pbs/dask-worker-space/worker-v3abka_l | |
[3]:
session = cc.database.create_session()
experiment = '01deg_jra55v13_ryf9091'
rho_0 = 1035.0 # kg/m^3 reference density
g = 9.81
# reduce computation by choosing only Southern Ocean latitudes
lat_range = slice(-70, -34.99)
Step 1: Load density and quantity being binned¶
(you can choose any other quantity instead of ty_trans, e.g. dzt. Interpolate density to whatever grid that variable is on)
For the simplicity of the demonstrations here, we will only load two months of monthly ty_trans, ty_trans_rho and pot_rho_2, then take the time average after we weight with the number of days in each month.
[4]:
start_time = '2170-01-01'
end_time = '2170-03-01'
time_slice = slice(start_time, end_time)
[5]:
%%time
ty_trans = cc.querying.getvar(experiment, 'ty_trans', session,
start_time = start_time, end_time = end_time)
ty_trans = ty_trans.sel(time = time_slice).sel(yu_ocean = lat_range)
# weighted time-mean by month length
days_in_month = ty_trans.time.dt.days_in_month
total_days = days_in_month.sum()
ty_trans = (ty_trans * days_in_month).sum('time') / total_days
CPU times: user 1.34 s, sys: 635 ms, total: 1.97 s
Wall time: 8.5 s
[6]:
%%time
pot_rho_2 = cc.querying.getvar(experiment, 'pot_rho_2', session,
start_time = start_time, end_time = end_time)
pot_rho_2 = pot_rho_2.sel(time = time_slice).sel(yt_ocean = lat_range)
pot_rho_2 = (pot_rho_2 * days_in_month).sum('time') / total_days
CPU times: user 494 ms, sys: 65.6 ms, total: 560 ms
Wall time: 6.28 s
[7]:
%%time
ty_trans_rho = cc.querying.getvar(experiment, 'ty_trans_rho', session,
start_time = start_time, end_time = end_time)
ty_trans_rho = ty_trans_rho.sel(time = time_slice).sel(grid_yu_ocean = lat_range)
ty_trans_rho = (ty_trans_rho * days_in_month).sum('time') / total_days
CPU times: user 290 ms, sys: 18.2 ms, total: 309 ms
Wall time: 602 ms
Create an xgcm grid for interpolation, and then interpolate density onto the meridional transport grid
[8]:
ds = xr.Dataset({'ty_trans': ty_trans, 'pot_rho_2': pot_rho_2})
grid = xgcm.Grid(ds, coords = {'Y': {'center': 'yt_ocean', 'right': 'yu_ocean'}}, periodic = False)
# interpolate density (t-grid) to ty_trans grid (xt_ocean and yu_ocean)
pot_rho_2 = grid.interp(pot_rho_2, 'Y', boundary = 'extend')
Method 1: xhistogram¶
We use xhistogram, described in https://xhistogram.readthedocs.io/en/latest/. It is a xarray aware method for computing histograms.
Computation in xhistogram occurs via the same method as in MOM5 online binning. It is thus most appropriate for an comparisons between offline and online binned quantities.
First, we define the edges of the target bins¶
Output will be an array with coordinate density the linear centre of these bins. If we choose potrho_edges, the end result will have coordinates potrho, which is the same as online binned ty_trans_rho.
[9]:
targetbins = cc.querying.getvar(experiment, 'potrho_edges', session, start_time = start_time, end_time = end_time,
n = 1, frequency = '1 monthly').values
Now apply the histogram over the vertical dimension st_ocean inside the target bins.¶
We include the variable we want to bin in weights. This quantity should be extensive, since grid cells vary in sizes, which is true because ty_trans is multiplied by the cell size in x and z directions.
[10]:
# Make sure the variables have a name, otherwise xhistogram doesn't know what to call the bins
ty_trans = ty_trans.rename('ty_trans')
pot_rho_2 = pot_rho_2.rename('pot_rho_2')
ty_trans_mean = histogram(pot_rho_2,
bins = [targetbins],
dim = ['st_ocean'],
weights = ty_trans).rename({pot_rho_2.name + '_bin': 'potrho',
'xt_ocean': 'grid_xt_ocean',
'yu_ocean': 'grid_yu_ocean'})
[11]:
%%time
ty_trans_mean = ty_trans_mean.load()
CPU times: user 12.8 s, sys: 2.76 s, total: 15.5 s
Wall time: 40.5 s
Now define meridional overturning streamfunctions as a cumulative sum of transport from the bottom of the ocean.¶
[12]:
def cumsum_from_bottom(residual):
cumsum = residual.cumsum('potrho') - residual.sum('potrho')
return cumsum
[13]:
%%time
psi_avg = cumsum_from_bottom(ty_trans_rho.sum('grid_xt_ocean') / (1e6 * rho_0)).load() # .load() since we'll use it a few times in this notebook
psi_avg_mean = cumsum_from_bottom(ty_trans_mean.sum('grid_xt_ocean') / (1e6 * rho_0))
CPU times: user 4.4 s, sys: 928 ms, total: 5.33 s
Wall time: 7.79 s
Plot streamfunctions of the residual, mean (what we just computed) and eddy (the difference) streamfunctions¶
[14]:
%%time
fig, axes = plt.subplots(nrows = 1, ncols = 3, figsize = (15, 4))
levels = np.linspace(-25, 25, 26)
psi_avg.plot.contourf(ax = axes[0], x = 'grid_yu_ocean', levels = levels, add_colorbar = False)
psi_avg_mean.plot.contourf(ax = axes[1], x = 'grid_yu_ocean', levels = levels, add_colorbar = False)
p = (psi_avg - psi_avg_mean).plot.contourf(ax = axes[2], x = 'grid_yu_ocean', levels = levels, add_colorbar = False)
cbar_ax = fig.add_axes([0.92, 0.15, 0.01, 0.7])
fig.colorbar(p, cax=cbar_ax, label='Transport (Sv)')
axes[0].set_title('Residual')
axes[1].set_title('Mean')
axes[2].set_title('Eddy')
for ax in axes:
ax.set_ylim(1037.5, 1032)
ax.set_xlim(-70, -35);
CPU times: user 176 ms, sys: 44.4 ms, total: 220 ms
Wall time: 229 ms
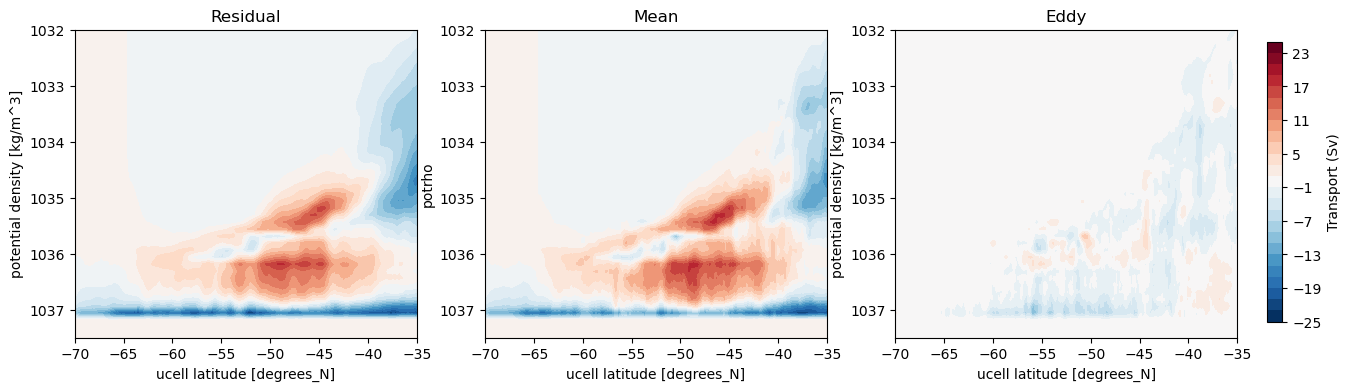
Method 2: xgcm¶
Use xgcm conservative binning, described in the tutorial available in xgcm documentation: https://xgcm.readthedocs.io/en/stable/transform.html
This method results in a smoother vertical distribution than xhistogram, as it is not quite a histogram but does some interpolation to the top and bottom of each vertical cell. We have found that the computation currently has issues with interior land boundaries: xgcm isn’t able to compute partial cells at the bottom of the ocean in MOM5. We thus add a correction after the computation to ensure that vertical integrals are preserved and thus that streamfunctions calculated are closed.
Load vertical grid bin centres and edges¶
[15]:
%%time
st_ocean = cc.querying.getvar(experiment, 'st_ocean', session, n=1)
st_edges_ocean = cc.querying.getvar(experiment, 'st_edges_ocean', session, n=1)
CPU times: user 1.36 s, sys: 180 ms, total: 1.54 s
Wall time: 2.24 s
Define edge of target density bins¶
[16]:
pot_rho_2_target = cc.querying.getvar(experiment, 'potrho_edges', session, start_time = start_time, end_time = end_time,
n=1, frequency = '1 monthly' ).values
Calculate vertical regridding into density coordinates¶
[17]:
%%time
ds = xr.Dataset({'ty_trans': ty_trans, 'pot_rho_2': pot_rho_2})
# Note: Quantity must be extensive, e.g., ty_trans, vhrho_nt, uhrho_et, tx_trans but *not*, e.g., v, salt.
# If not extensive, then we need to multiply by dzt or dzu.
ds = ds.assign_coords({'st_edges_ocean': st_edges_ocean})
ds = ds.chunk({'st_edges_ocean': 76, 'st_ocean': 75}) #xgcm doesn't like it if there is more than 1 chunk in this axis
grid = xgcm.Grid(ds, coords={'Z': {'center': 'st_ocean', 'outer': 'st_edges_ocean'}}, periodic = False)
ds['pot_rho_2_outer'] = grid.interp(ds.pot_rho_2, 'Z', boundary='extend')
ds['pot_rho_2_outer'] = ds['pot_rho_2_outer'].chunk({'st_edges_ocean': 76})
ty_trans_transformed_cons = grid.transform(ds.ty_trans,
'Z',
pot_rho_2_target,
method='conservative',
target_data=ds.pot_rho_2_outer)
### change name to fit previous bins because default xgcm naming is different
# pot_rho_2_outer is actually the CENTRE of bins (I guess the convention was defined for linear interpolation not conservative)
ty_trans_transformed_cons = ty_trans_transformed_cons.rename({'pot_rho_2_outer': 'potrho'})
CPU times: user 32.9 ms, sys: 559 µs, total: 33.5 ms
Wall time: 29.8 ms
[18]:
%%time
ty_trans_transformed_cons = ty_trans_transformed_cons.load()
CPU times: user 10.6 s, sys: 2.49 s, total: 13.1 s
Wall time: 24.9 s
Now account for partial cell at bottom¶
We do this by finding what is missing from the vertical integral (residual). This is what was in the partial cell. We then add that residual into the densest cell that currently exists in the transformed data. This is only an approximation, because the density of the partial cell may be denser than that of the cell above it. However, this correction means the vertical integral is preserved under the transformation.
[19]:
%%time
#find residual from vertical integral
ty_trans_residual = ty_trans.sum('st_ocean') - ty_trans_transformed_cons.sum('potrho') #this is positive definite
CPU times: user 605 ms, sys: 729 ms, total: 1.33 s
Wall time: 1.24 s
Find bottom density of ty_trans_transformed_cons¶
[20]:
%%time
# select out bottom values:
ty_trans_transformed_cons2 = ty_trans_transformed_cons.where(ty_trans_transformed_cons != 0)
dens_array = ty_trans_transformed_cons2 * 0 + ty_trans_transformed_cons2.potrho # array of isopycnal value where it exists and nan elsewhere
max_dens = dens_array.max(dim = 'potrho', skipna = True)
CPU times: user 1.12 s, sys: 1.06 s, total: 2.18 s
Wall time: 2.01 s
Add residual to this bottom density in array¶
[21]:
%%time
ty_trans_residual_array = (dens_array.where(dens_array == max_dens)*0 + 1)*ty_trans_residual
ty_trans_new = ty_trans_residual_array.fillna(0)+ ty_trans_transformed_cons
CPU times: user 1.93 s, sys: 1.25 s, total: 3.17 s
Wall time: 2.93 s
[22]:
# rename coords to match ty_trans_rho
ty_trans_new = ty_trans_new.rename({'yu_ocean': 'grid_yu_ocean', 'xt_ocean': 'grid_xt_ocean'})
[23]:
%%time
ty_trans_new = ty_trans_new.load()
CPU times: user 8.28 s, sys: 2.9 s, total: 11.2 s
Wall time: 28 s
Plot streamfunction of result¶
[24]:
psi_avg_mean_2 = cumsum_from_bottom(ty_trans_new.sum('grid_xt_ocean') / (1e6 * rho_0))
[25]:
%%time
fig, axes = plt.subplots(nrows = 1, ncols = 3, figsize = (15, 4))
levels = np.linspace(-25, 25, 26)
psi_avg.plot.contourf(ax = axes[0], x = 'grid_yu_ocean',levels = levels, add_colorbar = False)
psi_avg_mean_2.plot.contourf(ax = axes[1], x = 'grid_yu_ocean', levels = levels, add_colorbar = False)
p = (psi_avg - psi_avg_mean_2).plot.contourf(ax = axes[2], x = 'grid_yu_ocean', levels = levels, add_colorbar = False)
cbar_ax = fig.add_axes([0.92, 0.15, 0.01, 0.7])
fig.colorbar(p, cax=cbar_ax, label='Transport (Sv)')
axes[0].set_title('Residual')
axes[1].set_title('Mean')
axes[2].set_title('Eddy')
for ax in axes:
ax.set_ylim(1037.5, 1032)
ax.set_xlim(-70, -35);
CPU times: user 159 ms, sys: 18.7 ms, total: 178 ms
Wall time: 155 ms
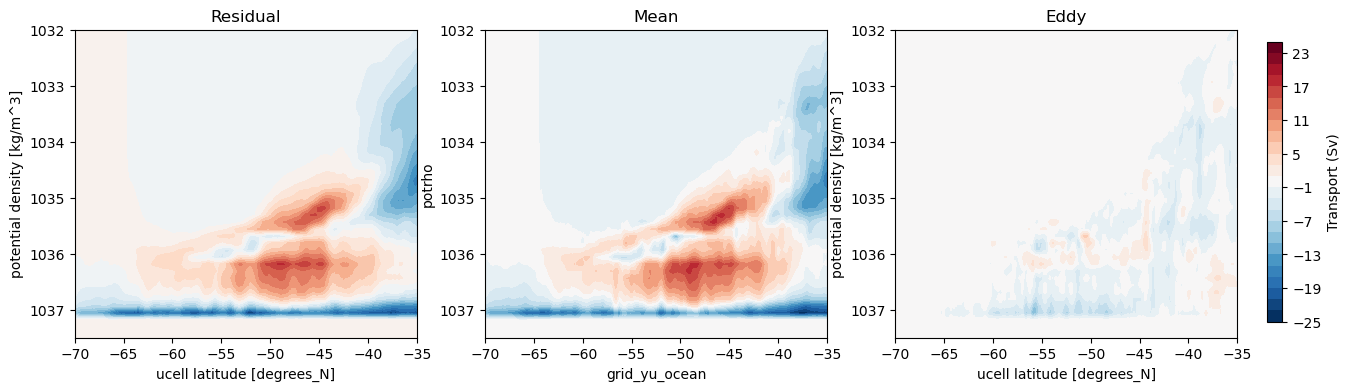
Method 3: Bin ty_trans (mean Eulerian overturning) into density bins¶
This uses the method by Lee et al. (2007) and which is is described as follows. Firstly, cells in the model output with a density \(\rho\) between two prescribed densities (\(\rho_\text{heavy} >\rho> \rho_\text{light}\)) are selected. Each cell is assigned a proximity to the lighter density \(\rho_\text{light}\), which is the ‘bin fraction’
Here, a bin fraction of 1 means the cell density \(\rho = \rho_\text{light}\) and \(f_b=0\) means \(\rho = \rho_\text{heavy}\). The quantity being binned, such as the meridional transport \(vh\), is then multiplied by \(f_b\) and added to the lighter density \(\rho_\text{light}\) bin’s meridional transport, followed by the \(vh(1-f_b)\) being added to the heavier bin, \(\rho_\text{heavy}\). This process is repeated for all sets of consecutive bins, meaning that density bins have input from model output cells with density slightly lower and higher than it.
Lee, M., Nurser, A., Coward, A., and De Cuevas, B. (2007). Eddy advective and diffusive transports of heat and salt in the Southern Ocean. Journal of Physical Oceanography, 37(5), 1376–1393.
For this method, we need to get rid of NaNs¶
[26]:
ty_trans = ty_trans.fillna(0)
pot_rho_2 = pot_rho_2.fillna(0)
Load first to reduce computation time¶
[27]:
%%time
pot_rho_2 = pot_rho_2.load()
ty_trans = ty_trans.load()
CPU times: user 9.4 s, sys: 2.98 s, total: 12.4 s
Wall time: 18.4 s
[28]:
# choose bins (in this case, default ty_trans_rho pot_rho_2 bins
rho2_bins = ty_trans_rho.potrho.values
# set up a zero array to be filled in by the algorithm
ty_trans_binned = np.zeros((len(rho2_bins), len(pot_rho_2.yu_ocean), len(pot_rho_2.xt_ocean)))
Note: the following cell takes a while.
[29]:
%%time
from tqdm.auto import tqdm
# loop over the bins, performing Lee et al. (2007) algorithm
# takes time, faster if ty_trans and pot_rho_2 already loaded
for i in tqdm(range(len(rho2_bins)-1)):
bin_mask = pot_rho_2.where(pot_rho_2 <= rho2_bins[i+1]).where(pot_rho_2 > rho2_bins[i])*0 + 1
bin_fractions = (rho2_bins[i+1] - pot_rho_2 * bin_mask)/(rho2_bins[i+1] - rho2_bins[i])
## bin ty_trans:
ty_trans_in_lower_bin = (ty_trans * bin_mask * bin_fractions).sum(dim = 'st_ocean')
ty_trans_binned[i, :, :] += ty_trans_in_lower_bin.fillna(0).values
del ty_trans_in_lower_bin
ty_trans_in_upper_bin = (ty_trans * bin_mask * (1-bin_fractions)).sum(dim = 'st_ocean')
ty_trans_binned[i+1, :, :] += ty_trans_in_upper_bin.fillna(0).values
del ty_trans_in_upper_bin
CPU times: user 6min 17s, sys: 7min 1s, total: 13min 18s
Wall time: 12min 18s
[30]:
# convert numpy array into xarray dataarray
ty_trans_binned_array = xr.DataArray(ty_trans_binned,
coords = [rho2_bins, pot_rho_2.yu_ocean, pot_rho_2.xt_ocean],
dims = ['potrho', 'grid_yu_ocean', 'grid_xt_ocean'],
name = 'ty_trans_binned')
[31]:
# find streamfunction
psi_avg_mean_3 = cumsum_from_bottom(ty_trans_binned_array.sum('grid_xt_ocean')) / (1e6 * rho_0)
Plot streamfunctions¶
[32]:
fig, axes = plt.subplots(nrows = 1, ncols = 3, figsize = (15, 4))
levels = np.linspace(-25, 25, 26)
psi_avg.plot.contourf(ax = axes[0], x = 'grid_yu_ocean',levels = levels, add_colorbar = False)
psi_avg_mean_3.plot.contourf(ax = axes[1], x = 'grid_yu_ocean', levels = levels, add_colorbar = False)
p = (psi_avg - psi_avg_mean_3).plot.contourf(ax = axes[2], x = 'grid_yu_ocean', levels = levels, add_colorbar = False)
cbar_ax = fig.add_axes([0.92, 0.15, 0.01, 0.7])
fig.colorbar(p, cax = cbar_ax, label = 'Transport (Sv)')
axes[0].set_title('Residual')
axes[1].set_title('Mean')
axes[2].set_title('Eddy')
for ax in axes:
ax.set_ylim(1037.5, 1032)
ax.set_xlim(-70, -35);
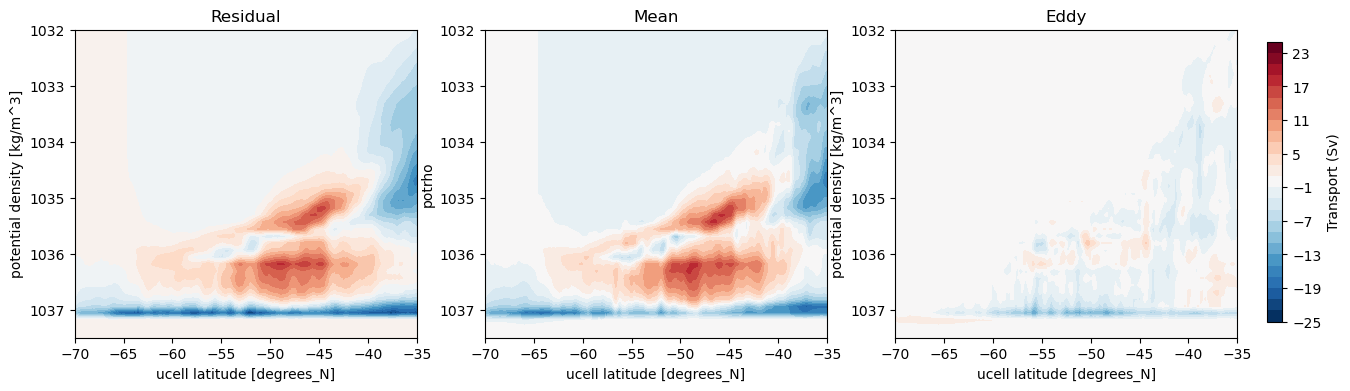
All three methods yield similar plots of the decomposition of the meridional overturning streamfunction.¶
The exact numbers resulting from the transformations differ, due to the different numerical methods. xhistogram is exact when compared to snapshots of MOM5 model output, and is hence most appropriate when comparing between online and offline binned quantities. xgcm and the Lee method can still be used to compare quantities binned offline. For example, if we were to instead bin the daily transports onto isopycnals and calculate eddy terms directly from the correlation of velocity and
thickness fluctuations, xgcm and the Lee method may be better as the weighted binning onto isopycnals leaves less chance of ‘gaps’ between density layers. The Lee method has no issues with partial cells, but it is much slower than xgcm.
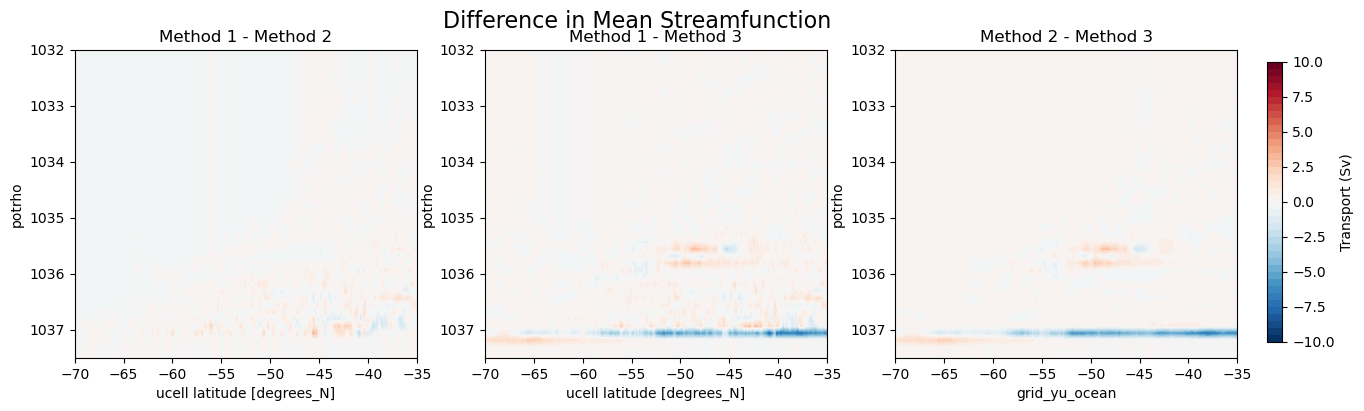
The difference in the mean streamfunction between the three methods is presented below.
[33]:
fig, axes = plt.subplots(nrows = 1, ncols = 3, figsize = (15, 4))
levels = np.arange(-10, 10.1, 0.5)
(psi_avg_mean-psi_avg_mean_2).plot.contourf(ax = axes[0], x = 'grid_yu_ocean',levels = levels, add_colorbar = False)
(psi_avg_mean-psi_avg_mean_3).plot.contourf(ax = axes[1], x = 'grid_yu_ocean', levels = levels, add_colorbar = False)
p = (psi_avg_mean_2 - psi_avg_mean_3).plot.contourf(ax = axes[2], x = 'grid_yu_ocean', levels = levels, add_colorbar = False)
cbar_ax = fig.add_axes([0.92, 0.15, 0.01, 0.7])
fig.colorbar(p, cax=cbar_ax, label='Transport (Sv)')
axes[0].set_title('Method 1 - Method 2')
axes[1].set_title('Method 1 - Method 3')
axes[2].set_title('Method 2 - Method 3')
for ax in axes:
ax.set_ylim(1037.5, 1032)
ax.set_xlim(-70, -35)
fig.suptitle('Difference in Mean Streamfunction', fontsize = 16);
An alternative method to calculate the decomposition of the residual meridional overturning circulation into mean and eddy components is to bin ty_trans (or vhrho_nt) into density bins using daily data (both density and transport). Then the transport \(\overline{vh}\) can be separated into a mean component \(\overline{v}\overline{h}\) and an eddy component \(\overline{v^\prime h^\prime}\), where the overline is a time average and primed quantities the deviation from the time
average. Quantities are calculated within density layers, and \(h\) is density layer thickness, calculated by binning dzt or dzu. This calculation, since it uses daily data, is computationally expensive and is difficult to do efficiently in a jupyter notebook. The resulting streamfunctions are similar, but not identical, and may be more intuitive for isopycnal flows. An example of this method can be found at
https://github.com/claireyung/Topographic_Hotspots_Upwelling-Paper_Code/blob/main/Figure_Code/Fig5-Overturning.ipynb.